🌙 数据结构和算法
掌握数据结构和算法,不管对于阅读框架源码,还是理解其背后的设计思想,都是非常有用的。
🌙 一、数据结构和算法
从广义上讲,数据结构就是指一组数据的存储结构。算法就是操作数据的一组方法。
从狭义上讲,是指某些著名的数据结构和算法,比如队列、栈、堆、二分查找、动态规划等。
数据结构是为算法服务的,算法要作用在特定的数据结构之上。
🌙 二、时间空间复杂度
复杂度分析是整个算法学习的精髓,只要掌握了它,数据结构和算法的内容基本上就掌握了一半。
🌙 1. 时间复杂度——大O表示法
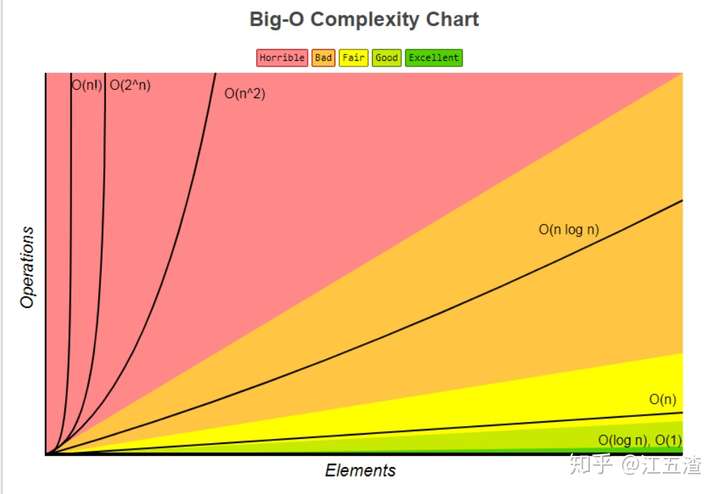
图:从经典算法题看时间复杂度 (opens new window)
如何理解算法时间复杂度的表示法,例如 O(n²)、O(n)、O(1)、O(nlogn) 等? (opens new window)
算法的时间复杂度(Time complexity)是一个函数,用于定性描述算法的运行时间。一般我们我们评估一个算法都是直接评估它的最坏的复杂度。
function sumN(n) {
let sum = 0;
let i=1;
for(;i<=n;i++) {
sum += i;
}
return sum;
}
2
3
4
5
6
7
8
假设每行代码执行的时间都一样为K,那么总时间:T(n) = (2 + n + n)*K = f(n) * K,即所有代码的执行时间 T(n) 与每行代码的执行次数n成正比。我们可以把这个规律总结成一个公式:
T(n) = O(f(n))
T(n) - 代码执行的时间
n - 数据规模的大小
f(n) - 每行代码执行的次数总和
O - 表示代码的执行时间 T(n) 与 f(n) 表达式成正比
2
3
4
5
6
🌙 2.时间复杂度分析
只关注循环执行次数最多的一段代码
加法法则:总复杂度等于量级最大的那段代码的复杂度
乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
大 O 这种复杂度表示方法只是表示一种变化趋势。我们通常会忽略掉公式中的常量、低阶、系数,只需要记录一个最大阶的量级就可以了。所以,我们在分析一个算法、一段代码的时间复杂度的时候,也只关注循环执行次数最多的那一段代码就可以了。这段核心代码执行次数的 n 的量级,就是整段要分析代码的时间复杂度。
即时间复杂度分析只需要关注复杂度量级最高的那部分即可。
🌙 3. 常见时间复杂度
| 度量级 | 大 O 表示 |
|---|---|
| 常量阶 | |
| 对数阶 | |
| 线性阶 | |
| 线性对数阶 | |
| 平方阶 | |
| 立方阶 | |
| 指数阶 | |
| 阶乘阶 |
一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是Ο(1)。
在对数阶时间复杂度的表示方法里,我们忽略对数的“底”,统一表示为 O(logn)
🌙 4.空间复杂度分析
时间复杂度的全称是渐进时间复杂度,表示算法的执行时间与数据规模之间的增长关系。
类比一下,空间复杂度全称就是渐进空间复杂度(asymptotic space complexity),表示算法的存储空间与数据规模之间的增长关系。
常见的空间复杂度就是 O(1)、O(n)、O(n ),像 O(logn)、O(nlogn) 这样的对数阶复杂度平时都用不到。而且,空间复杂度分析比时间复杂度分析要简单很多。
🌙 5.最好、最坏、平均、均摊时间复杂度
分析下面函数的时间复杂度:
function find(arr, x) {
let i=0;
let index = -1;
let len = arr.length;
for(;i<len;i++) {
if(arr[i]===x) {
index = i;
}
}
return pos;
}
2
3
4
5
6
7
8
9
10
11
这段代码要实现的功能是,在一个无序的数组(array)中,查找变量x 出现的位置。如果没有找到,就返回 -1。这段代码的复杂度是 O(n),其中,n 代表数组的长度。
我们在数组中查找一个数据,并不需要每次都把整个数组都遍历一遍,因为有可能中途找到就可以提前结束循环了。但是,这段代码写得不够高效。我们可以这样优化一下这段查找代码:
function find(arr, x) {
let i=0;
let index = -1;
let len = arr.length;
for(;i<len;i++) {
if(arr[i]===x) {
index = i;
break;
}
}
return pos;
}
2
3
4
5
6
7
8
9
10
11
12
因为,要查找的变量 x 可能出现在数组的任意位置。如果数组中第一个元素正好是要查找的变量 x,那就不需要继续遍历剩下的 n-1 个数据了,那时间复杂度就是 O(1)。但如果数组中不存在变量 x,那我们就需要把整个数组都遍历一遍,时间复杂度就成了 O(n)。所以,不同的情况下,这段代码的时间复杂度是不一样的。
最好情况时间复杂度(best case time complexity):在最理想的情况下,执行这段代码的时间复杂度
最坏情况时间复杂度(worst case time complexity):在最糟糕的情况下,执行这段代码的时间复杂度
平均情况时间复杂度(average case time complexity):加权平均时间复杂度或者期望时间复杂度(与概率相关)
均摊时间复杂度(amortized time complexity):均摊时间复杂度就是一种特殊的平均时间复杂度
🌙 三、数组Array (opens new window)
数组访问速度快
数组(Array)是一种线性表数据结构。它用一组连续的内存空间,来存储一组具有相同类型的数据。它具有连续的内存空间,可以进行“随机访问”。但有利就有弊,比如要想在数组中删除、插入一个数据,为了保证连续性,就需要做大量的数据搬移工作。
线性表(Linear List)。顾名思义,线性表就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。其实除了数组,链表、队列、栈等也是线性表结构。
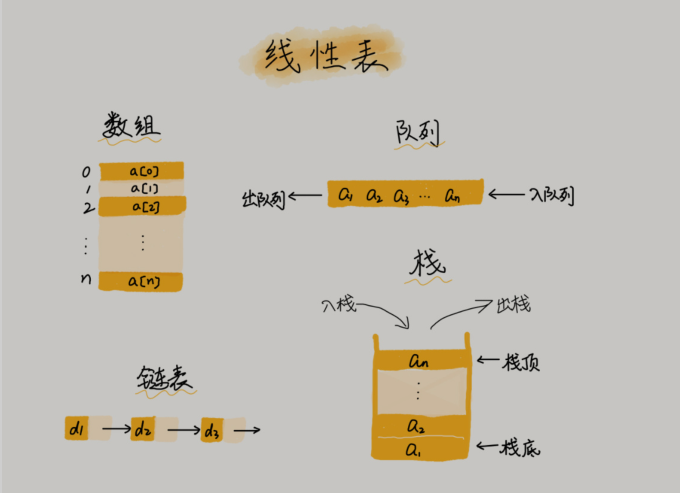
非线性表,比如二叉树、堆、图等。之所以叫非线性,是因为,在非线性表中,数据之间并不是简单的前后关系。
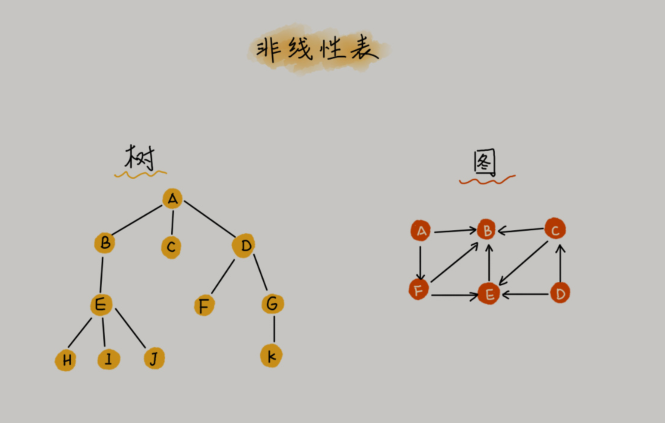
一般认为:“链表适合插入、删除,时间复杂度 O(1);数组适合查找,查找时间复杂度为O(1)”。
这种表述是不准确的,数组是适合查找操作,但是查找的时间复杂度并不为O(1)。即便是排好序的数组,你用二分查找,时间复杂度也是 O(logn)。所以,正确的表述应该是,数组支持随机访问,根据下标随机访问的时间复杂度为 O(1)。
🌙 四、链表LinkedList (opens new window)
插入和删除速度快
数组需要一块连续的内存空间来存储,对内存的要求比较高。
链表恰恰相反,它并不需要一块连续的内存空间,它通过“指针”将一组零散的内存块串联起来使用。
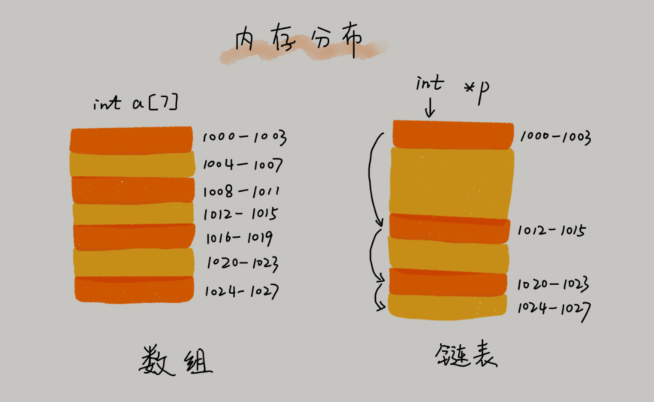
链表通过指针将一组零散的内存块串联在一起。其中,我们把内存块称为链表的“结点”。为了将所有的结点串起来,每个链表的结点除了存储数据之外,还需要记录链上的下一个结点的地址。如图所示,我们把这个记录下个结点地址的指针叫作后继指针next。
习惯性地把第一个结点叫作头结点,把最后一个结点叫作尾结点。其中,头结点用来记录链表的基地址。有了它,我们就可以遍历得到整条链表。而尾结点特殊的地方是:指针不是指向下一个结点,而是指向一个空地址 NULL,表示这是链表上最后一个结点。
与数组一样,链表也支持数据的查找、插入和删除操作,而且很高效:
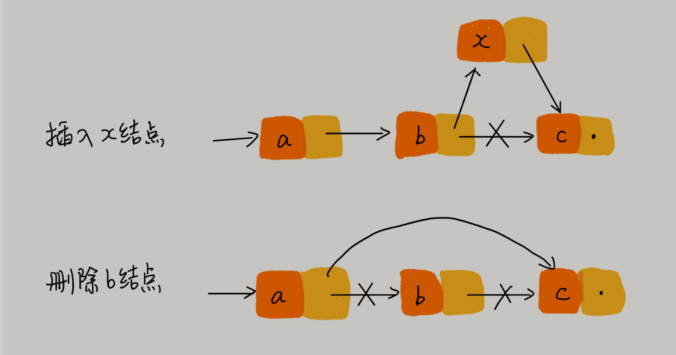
链表随机访问的性能没有数组好,需要 O(n) 的时间复杂度。因为链表中的数据并非连续存储的,所以无法像数组那样,根据首地址和下标,通过寻址公式就能直接计算出对应的内存地址,而是需要根据指针一个结点一个结点地依次遍历,直到找到相应的结点。
最常见的链表结构,它们分别是:单链表、双向链表和循环链表。
🌙 1.单链表
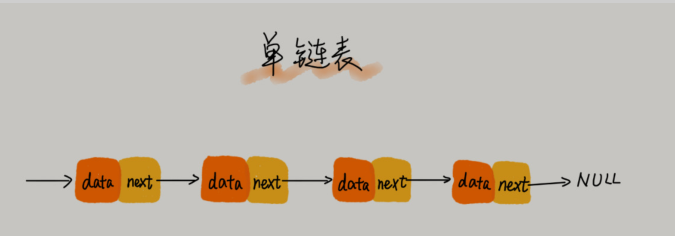
🌙 2.循环链表
循环链表是一种特殊的单链表。实际上,循环链表也很简单。它跟单链表唯一的区别就在尾结点。
我们知道,单链表的尾结点指针指向空地址,表示这就是最后的结点了。而循环链表的尾结点指针是指向链表的头结点。从循环链表图中,你应该可以看出来,它像一个环一样首尾相连,所以叫作“循环”链表。
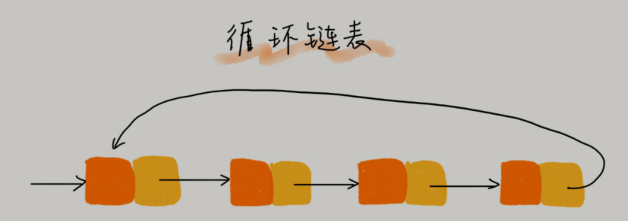
和单链表相比,循环链表的优点是从链尾到链头比较方便。当要处理的数据具有环型结构特点时,就特别适合采用循环链表。比如著名的约瑟夫问题 (opens new window)。尽管用单链表也可以实现,但是用循环链表实现的话,代码就会简洁很多。
🌙 3.双向链表
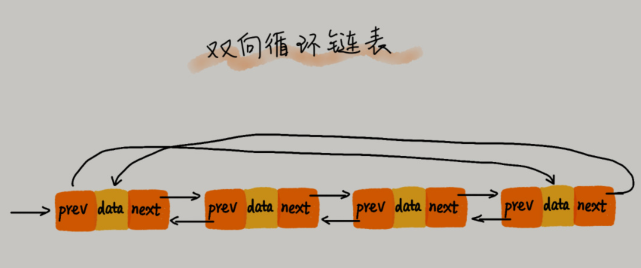
单向链表只有一个方向,结点只有一个后继指针 next 指向后面的结点。而双向链表,顾名思义,它支持两个方向,每个结点不止有一个后继指针 next 指向后面的结点,还有一个前驱指针 prev 指向前面的结点。
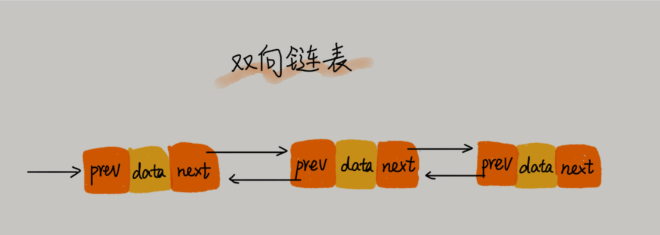
从图中可以看出,双向链表需要额外的两个空间来存储后继结点和前驱结点的地址。所以,如果存储同样多的数据,双向链表要比单链表占用更多的内存空间。虽然两个指针比较浪费存储空间,但可以支持双向遍历,这样也带来了双向链表操作的灵活性。
从结构上来看,双向链表可以支持 O(1) 时间复杂度的情况下找到前驱结点,正是这样的特点,也使双向链表在某些情况下的插入、删除等操作都要比单链表简单、高效。
🌙 4.双向循环链表
🌙 5.数组VS链表
| 时间复杂度 | 数组 | 链表 |
|---|---|---|
| 插入删除 | O(n) | O(1) |
| 随机访问 | O(1) | O(n) |
🌙 6.JS实现链表
🌙 6.1 单链表
单链表中的节点应该具有两个属性:val 和 next。val 是当前节点的值,next 是指向下一个节点的指针/引用。如果要使用双向链表,则还需要一个属性 prev 以指示链表中的上一个节点。
// 定义节点类
class Node {
constructor(val) {
this.val = val;
this.next = null;
}
}
// 定义链表类
class LinkedList {
constructor(){
this.head = null;
this.length = 0;
}
append(val) {}
insert(position,val) {}
indexOf(val){}
removeAt(position){}
isEmpty(){}
size(){}
toString(){}
getHead(){}
getTail(){}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
需要实现的方法:
- [x]
append(element):向列表尾部添加一个新的项。 - [x] insert(position, val) :向列表的特定位置插入一个新的项。
- [x]
remove(val):从列表中移除一项。 - [x]
indexOf(val):返回元素在列表中的索引。如果列表中没有该元素则返回 -1 。 - [x]
removeAt(position):从列表的特定位置(从0开始,0表示第一个元素)移除一项。 - [x]
isEmpty():如果链表中不包含任何元素,返回 true ,如果链表长度大于0则返回 false 。 - [x]
size():返回链表包含的元素个数。与数组的 length 属性类似。 - [x]
toString():由于列表项使用了 Node 类,就需要重写继承自JavaScript对象默认的toString 方法,让其只输出元素的值。 - [x]
getHead():获取head - [ ]
getTail():获取tail
// 定义节点类
class Node {
constructor(val) {
this.val = val;
this.next = null;
}
}
// 定义链表类
class LinkedList {
constructor(){
this.head = null;
this.tail = null;
this.length = 0;
}
// 向链表尾部追加元素
append(val) {
let node = new Node(val);
let current = null;
this.tail = node;
if(this.head === null) {
// 链表中第一个节点
this.head = node;
} else {
current = this.head;
// 循环列表,直到找到最后一项
while(current.next) {
current = current.next;
}
//找到最后一项,将其next赋为node,建立链接
current.next = node;
}
return ++this.length;
}
// 从链表中移除第几个元素
removeAt(position) {
// 检查越界值
if(position > -1 && position < this.length) {
let current = this.head;
let previous = null;
// 移除第一项
if(position === 0) {
this.head = current.next;
if (this.length === 1) {
this.tail = null;
}
} else {
// 从head顺延找到目标
while(position--) {
previous = current;
current = current.next;
}
// 将previous与current的下一项链接起来:跳过current,从而移除它
previous.next = current.next
}
// 更新size
this.length--;
return current.val;
} else {
return null;
}
}
// 向列表的任意位置插入一个新的项
insert(position, val) {
// 检查越界值
if(position >= 0 && position <= this.length) {
let node = new Node(val);
let current = this.head;
let previous = null;
// 在第一个位置添加
if(position === 0) {
if (!this.head) { //新增的
this.head = node;
this.tail = node;
} else {
node.next = current;
this.head = node;
}
} else if (position === length) {
current = this.tail;
current.next = node;
this.tail = node;
}else {
// 在其他位置添加
while(--position) {
previous = current;
current = current.next;
}
node.next = current;
previous.next = node;
}
this.length++;
return true;
} else {
// 更新size
return false;
}
}
// toString 方法会把 LinkedList 对象转换成一个字符串
toString() {
let current = this.head;
let str = current ? current.val : '';
while(current && current.next) {
current = current.next;
str += '->' + current.val;
}
return str;
}
// indexOf 方法接收一个元素的值,如果在列表中找到它,就返回元素的位置,否则返回 -1
indexOf(val) {
let current = this.head;
let index = 0;
while(current) {
if(val === current.val) {
return index;
}
current = current.next;
index++;
}
return -1;
}
// remove删除一个指定的元素值
remove(val) {
let index = this.indexOf(val);
return this.removeAt(index);
}
// isEmpty判空
isEmpty() {
return this.length === 0;
}
// size返回长度
size() {
return this.length;
}
// getHead获取head
getHead(){
return this.head;
}
// getHead获取tail
getTail(){
return this.tail;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
测试一波:
let lk = new LinkedList();
lk.append(1); // 1
lk.append(2); // 2
lk.insert(0,0); // true
lk.toString(); // '0->1->2'
lk.getHead(); // Node {val: 0, next: Node}
lk.getTail(); // Node {val: 2, next: Node}
lk.size(); // 3
lk.isEmpty(); // false
lk.indexOf(0); // 0
lk.indexOf(4); // -1
lk.remove(0);
lk.toString(); // '1->2'
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
🌙 6.2 双向链表
双向链表和普通链表的区别在于,在链表中,一个节点只有链向下一个节点的链接,而在双向链表中,链接是双向的:一个链向下一个元素,另一个链向前一个元素。
// 定义节点类
class Node {
constructor(val) {
this.val = val;
this.next = null;
// 增加prev
this.prev = null;
}
}
// 定义链表类
class DoubleLinkedList {
constructor(){
this.head = null;
// 增加tail
this.tail = null;
this.length = 0;
}
// 向链表尾部追加元素
append(val) {
let node = new Node(val);
let current = null;
// 新增
this.tail = node;
if(this.head === null) {
// 链表中第一个节点
this.head = node;
} else {
//找到最后一项,将其next赋为node,建立链接
current = this.tail;
current.next = node;
node.prev = current;
}
return ++this.length;
}
// 从链表中移除第几个元素
removeAt(position) {
// 检查越界值
if(position > -1 && position < this.length) {
let current = this.head;
let previous = null;
// 移除第一项
if(position === 0) {
this.head = current.next;
//如果只有一项,更新tail //新增的
if(this.length===1) {
this.tail = null;
} else {
this.head.prev = null;
}
//最后一项 //新增的
} else if(position === this.length -1) {
current = this.tail;
this.tail = current.prev;
this.tail.next = null;
} else {
// 从head顺延找到目标
while(--position) {
previous = current;
current = current.next;
}
// 将previous与current的下一项链接起来:跳过current,从而移除它
previous.next = current.next;
current.next.prev = previous; //新增的
}
// 更新size
this.length--;
return current.val;
} else {
return null;
}
}
// 向列表的任意位置插入一个新的项
insert(position, val) {
// 检查越界值
if(position > -1 && position <= this.length) {
let node = new Node(val);
let current = this.head;
let previous = null;
// 在第一个位置添加
if(position === 0) {
if (!this.head){ //新增的
this.head = node;
this.tail = node;
} else {
node.next = current;
current.prev = node;//新增的
this.head = node;
}
} else if (position === length) {
current = this.tail;
current.next = node;
node.prev = current;
this.tail = node;
} else {
// 在其他位置添加
while(position--) {
previous = current;
current = current.next;
}
node.next = current;
previous.next = node;
// 新增的
current.prev = node;
node.prev = previous;
}
this.length++;
return true;
} else {
// 更新size
return false;
}
}
// toString 方法会把 LinkedList 对象转换成一个字符串
toString() {
let current = this.head; // 有可能为null
let str = current ? current.val : '';
while(current && current.next) {
current = current.next;
str += '->' + current.val;
}
return str;
}
// indexOf 方法接收一个元素的值,如果在列表中找到它,就返回元素的位置,否则返回 -1
indexOf(val) {
let current = this.head;
let index = 0;
while(current) {
if(val === current.val) {
return index;
}
current = current.next;
index++;
}
return -1;
}
// remove删除一个指定的元素值
remove(val) {
let index = this.indexOf(val);
return this.removeAt(index);
}
// isEmpty判空
isEmpty() {
return this.length === 0;
}
// size返回长度
size() {
return this.length;
}
// getHead获取head
getHead(){
return this.head;
}
// getTail获取tail
getTail(){
return this.tail;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
🌙 五、栈Stack (opens new window)
🌙 1.栈的引出:如何实现浏览器的前进和后退功能?
浏览器的前进、后退功能,我想你肯定很熟悉吧?
假设你是 Chrome 浏览器的开发工程师,你会如何实现这个功能呢?
—— 使用栈来实现:
我们使用两个栈,X 和 Y,我们把首次浏览的页面依次压入栈 X,当点击后退按钮时,再依 次从栈 X 中出栈,并将出栈的数据依次放入栈 Y。当我们点击前进按钮时,我们依次从栈Y 中取出数据,放入栈 X 中。当栈 X 中没有数据时,那就说明没有页面可以继续后退浏览了。当栈 Y 中没有数据,那就说明没有页面可以点击前进按钮浏览了。
🌙 2.如何理解“栈”?
一般会把队列和栈放一起比较,前者先进先出(FIFO),后者先进后出(LIFO)。

从栈的操作特性上来看,栈是一种“操作受限”的线性表,只允许在一端插入和删除数据。我们可以使用数组或链表替代栈,但是两者暴露了太多接口,意味着更灵活,有时候更灵活反而导致容易出错,不可控。存在即合理,栈自然有它的用武之地。
当某个数据集合只涉及在一端插入和删除数据,并且满足后进先出、先进后出的特性,我们就应该首选“栈”这种数据结构。
🌙 3.JS实现栈
class Stack {
constructor() {
this.length = 0;
this.data = [];
}
// 入栈
push(val){
this.data.push(val);
this.length++;
return val;
}
// 出栈
pop() {
if(this.length > 0) {
this.length--;
return this.data.pop();
}
}
// 判空
isEmpty() {
return this.length === 0;
}
// 获取长度
size() {
return this.length;
}
// 获取栈顶元素
top() {
return this.data[this.length - 1]
}
// 获取栈底元素
bottom(){
return this.data[0];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
🌙 4.用栈实现队列
class QueenByStack {
constructor() {
// 入队列-栈
this.stack1 = new Stack();
// 出队列栈
this.stack2 = new Stack();
}
// 入队列
enqueue(value) {
this.stack1.push(value);
return value;
}
// 出队列
dequeue() {
// 将stack1的数据放入stack2(从而完成将stack1队首和队尾调换位置)
while(!this.stack1.isEmpty()){
this.stack2.push(this.stack1.pop())
}
// 此时stack2的队尾就是最先进入队列的元素,出栈即出队列
const top = this.stack2.pop();
// 再将剩余的数据还原
while(!this.stack2.isEmpty()) {
this.stack1.push(this.stack2.pop())
}
return top;
}
// 获取队列头部
getHead() {
return this.stack1.bottom();
}
// 获取队列尾部
getTail() {
return this.stack1.top();
}
// 判空
isEmpty() {
return this.stack1.isEmpty();
}
// 获取长度
size() {
return this.stack1.size();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
🌙 六、队列Queue (opens new window)
🌙 1.如何理解“队列”?
队列这个概念非常好理解。你可以把它想象成排队买票,先来的先买,后来的人只能站末尾,不允许插队。先进者先出,这就是典型的“队列”。先进先出(FIFO)

我们知道,栈只支持两个基本操作:入栈 push()和出栈 pop()。
队列跟栈一样,也是一种操作受限的线性表数据结构。最基本的操作也是两个:入队 enqueue(),放一个数据到队列尾部;出队 dequeue(),从队列头部取一个元素。
秘诀:“吃多了拉就是队列,吃多了吐就是栈”
🌙 2.JS实现简单队列
跟栈一样,队列可以用数组来实现,也可以用链表来实现。用数组实现的栈叫作顺序栈,用链表实现的栈叫作链式栈。同样,用数组实现的队列叫作顺序队列,用链表实现的队列叫作链式队列。
🌙 2.1 顺序队列
使用数组来实现队列:
class Queue {
constructor() {
this.data = [];
}
// 入队列
enqueue(value) {
this.data.push(value);
return true;
}
// 出队列
dequeue() {
if(this.data.length > 0) {
this.data.shift();
return true;
}
return false
}
// 获取队列头部
getHead() {
return this.data[0];
}
// 获取队列尾部
getTail() {
return this.data[this.data.length - 1];
}
// 判空
isEmpty() {
return this.data.length === 0;
}
// 获取长度
size() {
return this.data.length
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
🌙 2.2 链式队列
使用链表来实现队列:
class Queue {
constructor() {
this.data = new LinkedList();
}
// 入队列
enqueue(value) {
this.data.append(value);
return true;
}
// 出队列
dequeue() {
if(this.data.size() > 0) {
this.data.removeAt(0);
return true;
}
return false
}
// 获取队列头部
getHead() {
return this.data.getHead();
}
// 获取队列尾部
getTail() {
return this.data.getTail();
}
// 判空
isEmpty() {
return this.data.isEmpty();
}
// 获取长度
size() {
return this.data.size();
}
toString() {
return this.data.toString();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
🌙 3.JS实现循环队列 (opens new window)
循环队列是一种线性数据结构,其操作表现基于 FIFO(先进先出)原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里,一旦一个队列满了,我们就不能插入下一个元素,即使在队列前面仍有空间。但是使用循环队列,我们能使用这些空间去存储新的值。
- [x]
CircularQueue(k): 构造器,设置队列长度为 k 。 - [x]
getHead: 从队首获取元素。如果队列为空,返回 -1 。 - [x]
getTail: 获取队尾元素。如果队列为空,返回 -1 。 - [x]
enqueue(value): 向循环队列插入一个元素。如果成功插入则返回真。 - [x]
dequeue(): 从循环队列中删除一个元素。如果成功删除则返回真。 - [x]
isEmpty(): 检查循环队列是否为空。 - [x]
isFull(): 检查循环队列是否已满。
class CircularQueue {
constructor(k) {
this.size = k;
this.data = Array(k);
// 头部指针(从-1开始是为了减少一个数组空间的浪费)
this.head = -1;
// 尾部指针
this.tail = -1;
}
getHead() {
if(this.isEmpty()) {
return -1;
}
return this.data[this.head];
}
getTail() {
if(this.isEmpty()) {
return -1;
}
return this.data[this.tail];
}
// 入队列时,更新tail
enqueue(value) {
if(this.isFull()) {
return false;
}
// 只有在队列当为空时,更新head
if(this.isEmpty()) {
this.head = 0;
}
this.tail = (this.tail + 1) % this.size;
this.data[this.tail] = value;
return true;
}
// 出队列时,更新head
dequeue() {
if(this.isEmpty()) {
return false;
}
// 出队列时,当首尾相遇时,表示队列为空了,还原head和tail
if(this.head === this.tail) {
this.head = -1;
this.tail = -1;
return true;
}
this.head = (this.head + 1) % this.size;
return true;
}
isEmpty() {
// 头部指针指向-1,此时队列为空
return this.head === -1;
}
isFull() {
// 尾部指针下一位为头部指针,表示对列满了
return ((this.tail + 1) % this.size) === this.head;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
测试一波:
let circularQueue = new CircularQueue(3); // 设置长度为 3
circularQueue.enqueue(1); // 返回 true
circularQueue.enqueue(2); // 返回 true
circularQueue.enqueue(3); // 返回 true
circularQueue.enqueue(4); // 返回 false,队列已满
circularQueue.getTail(); // 返回 3
circularQueue.isFull(); // 返回 true
circularQueue.dequeue(); // 返回 true
circularQueue.enqueue(4); // 返回 true
circularQueue.getTail(); // 返回 4
2
3
4
5
6
7
8
9
10
🌙 4.用队列实现栈
class StackByQueue {
constructor() {
// 这里是顺序队列(数组实现)
this.queue = new Queue();
}
// 入栈
push(val){
this.queue.enqueue(val);
return val;
}
// 出栈
pop() {
if(!this.queue.isEmpty()) {
let ret = [];
// 获取栈顶元素(队尾元素)
const top = this.top();
while(this.size() > 1) {
// 除了队尾,其他出队列
ret.push(this.queue.dequeue());
}
this.queue = ret;
return top;
}
}
// 判空
isEmpty() {
return this.queue.isEmpty();
}
// 获取长度
size() {
return this.queue.size();
}
// 获取栈顶元素
top() {
return this.queue.getTail();
}
// 获取栈底元素
bottom(){
return this.queue.getHead();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
🌙 七、树Tree (opens new window)
数组、栈、队列、链表都是线性表结构,树是一种非线性结构。
树是一种抽象数据类型(ADT)或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由 n(n>0)n(n>0) 个有限节点组成一个具有层次关系的集合。
把它叫做「树」是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
它具有以下的特点:
- 每一个非根节点有且只有一个父节点;
- 每个节点都只有有限个子节点或无子节点;
- 没有父节点的节点称为根节点;
- 没有子节点的叫做叶子节点;
- 除了根节点外,每个子节点可以分为多个不相交的子树;
- 树里面没有环路。(有环的话,就是图了)
节点名称:
- 父节点:A是B的父节点
- 子节点:B是A的子节点
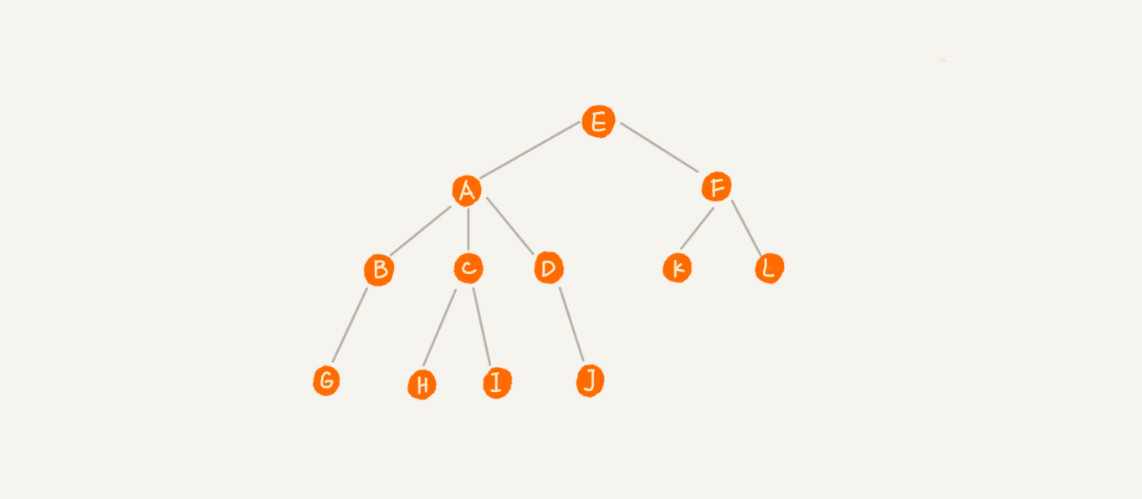
- 兄弟节点:B、C、D 这三个节点的父节点是同一个节点,他们是兄弟节点
- 叶子节点:没有子节点的节点叫作叶子节点或者叶节点,比如图中的 G、H、I、J、K、L 都是叶子节点。
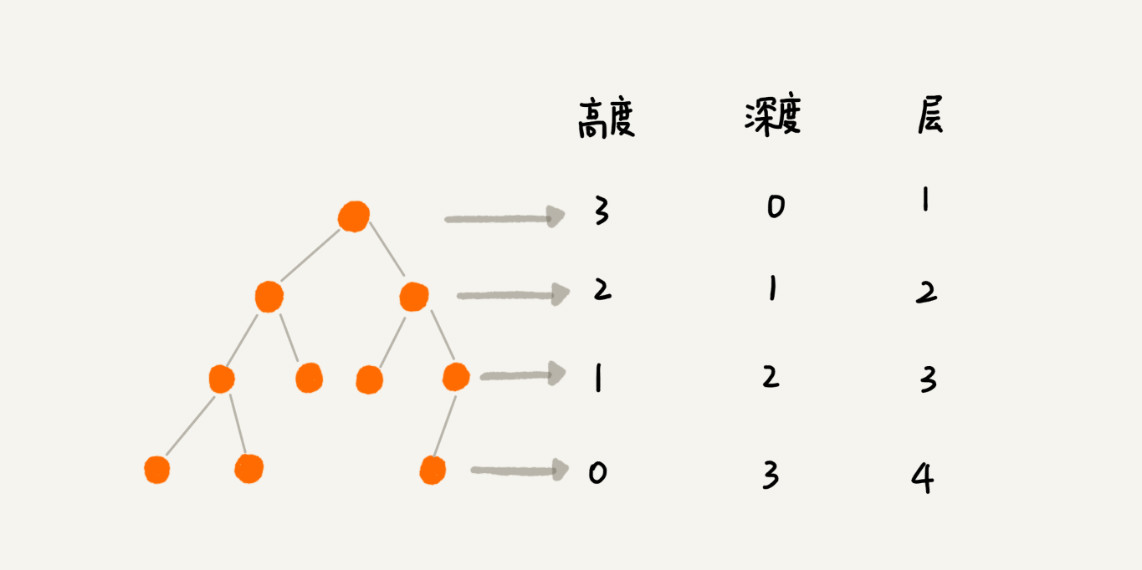
三个概念:
- 节点的高度(height):节点到叶子节点的最长路径(从0开始)
- 节点的深度(depth):根节点到该节点的路径长度(从0开始)
- 节点的层级(level):节点的深度 + 1(从1开始)
- 树的高度:即根节点的高度
🌙 1.二叉树
二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子节点和右子节点。
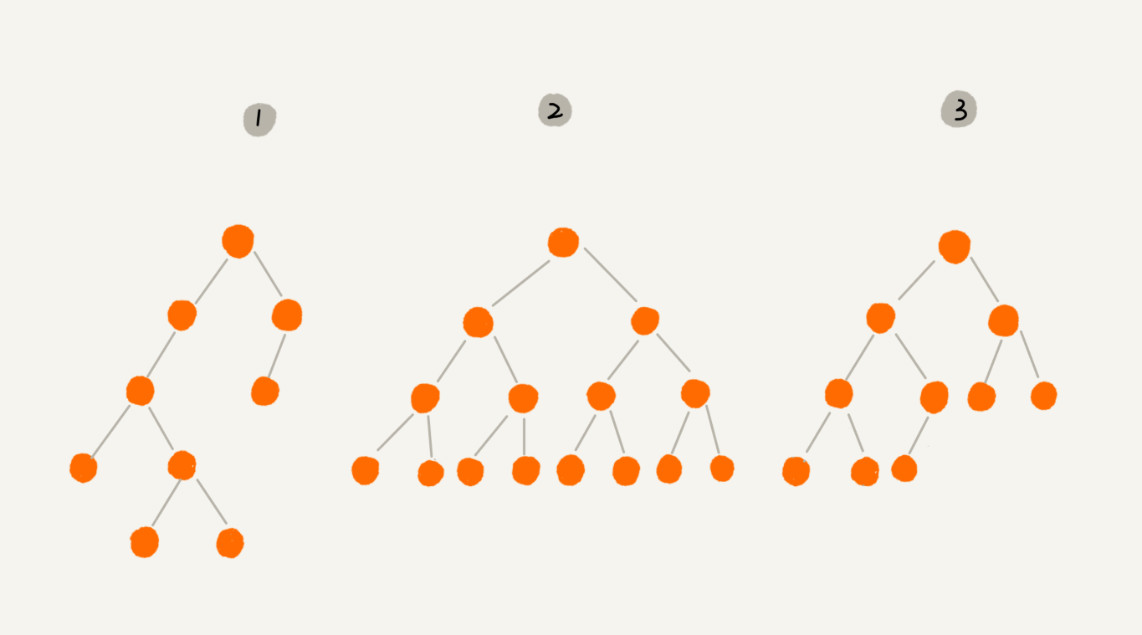
满二叉树:叶子节点全都在最底层,除了叶子节点之外,每个节点都有左右两个子节点,这种二叉树就叫作满二叉树。(如:编号2)
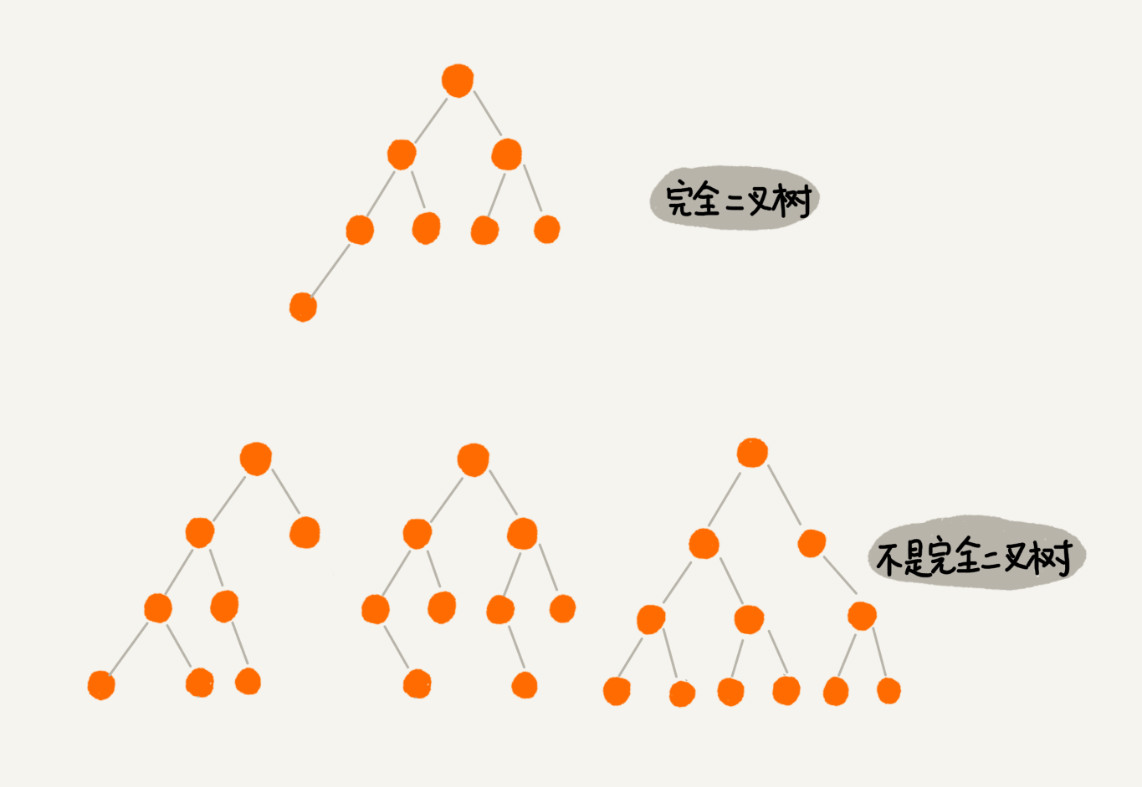
完全二叉树:叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大,这种二叉树叫作完全二叉树。(如编号3)
🌙 2. 二叉树的存储
如何表示(或者存储)一棵二叉树?
想要存储一棵二叉树,我们有两种方法,一种是基于指针或者引用的二叉链式存储法,一种 是基于数组的顺序存储法。
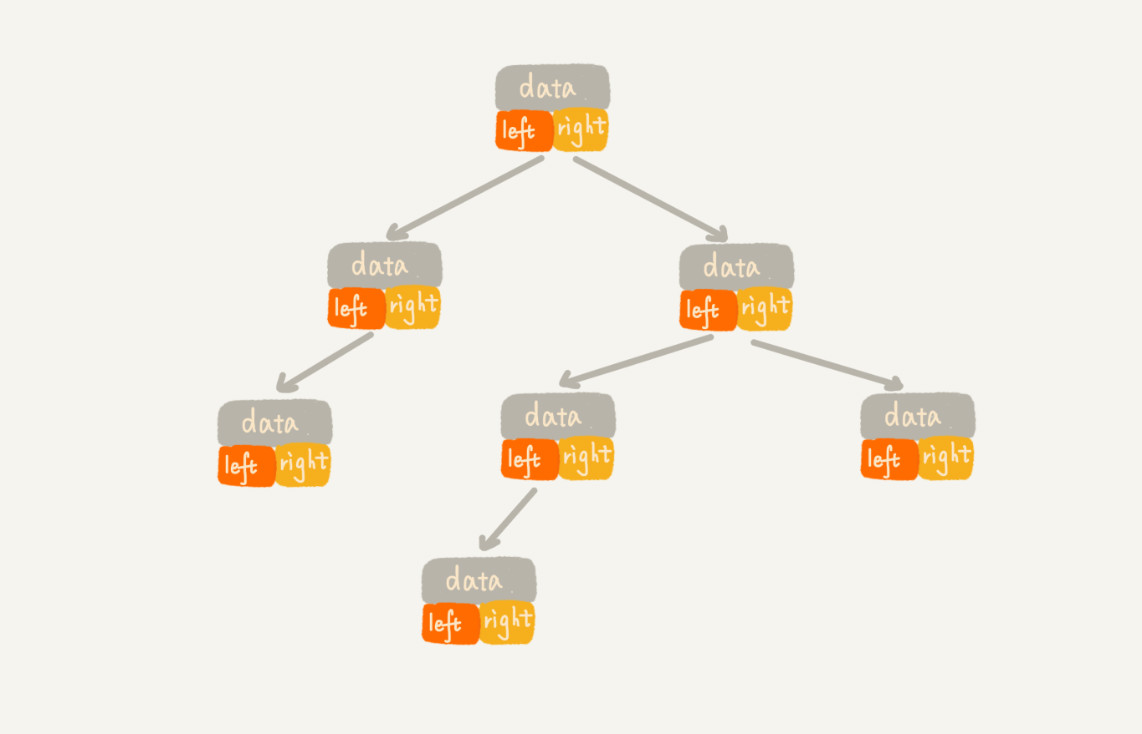
链式存储法:每个节点有三个字段,其中一个存储数据,另外两个是指向左右子节点的指针。
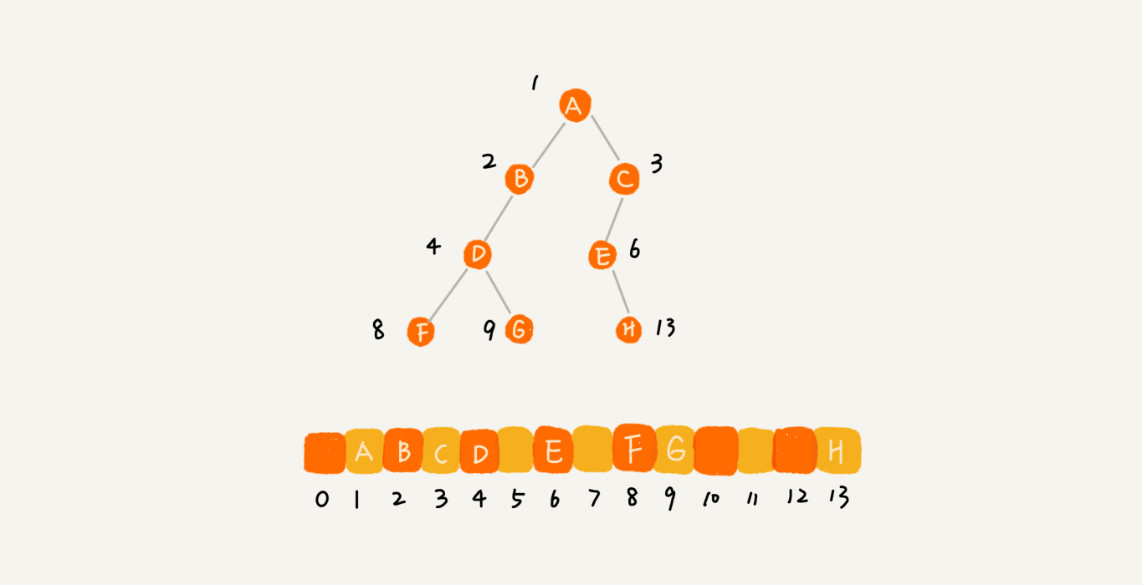
顺序存储法:把根节点存储在下标 i = 1 的位置,那左子节点存储在下标 2 * i = 2 的位置,右子节点存储在 2 * i + 1 = 3 的位置。以此类推,B 节点的左子节点存储在 2 * i = 2 * 2 = 4 的位置,右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5 的位置。
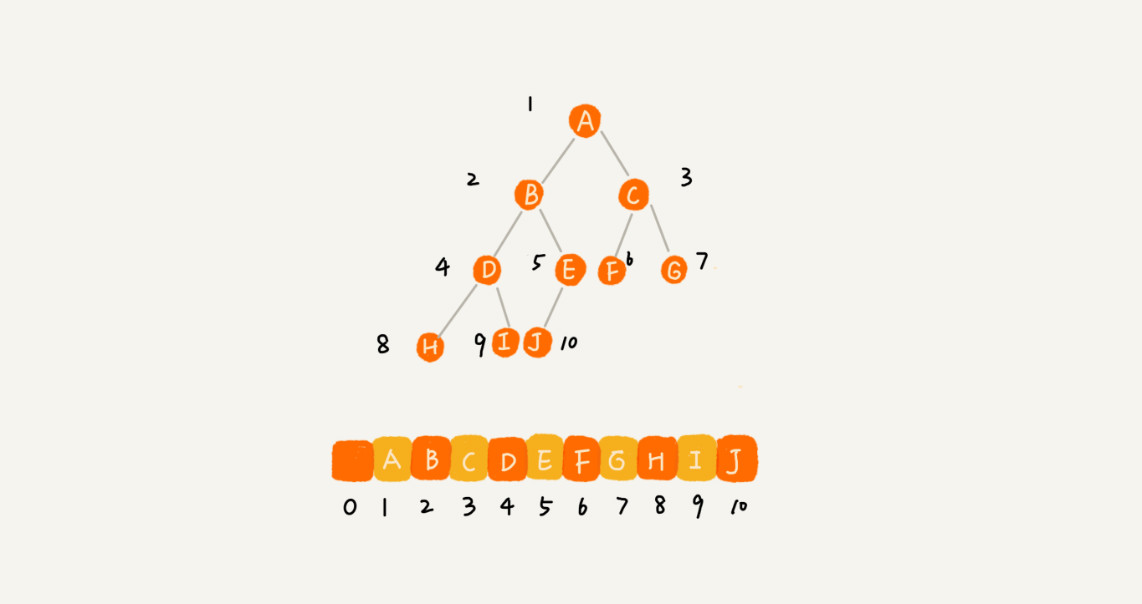
不过,我刚刚举的例子是一棵完全二叉树,所以仅仅“浪费”了一个下标为 0 的存储位置。如果是非完全二叉树,其实会浪费比较多的数组存储空间。你可以看我举的下面这个例子。
/* 数组表示下的二叉树类 */
class ArrayBinaryTree {
#tree: (number | null)[];
/* 构造方法 */
constructor(arr: (number | null)[]) {
this.#tree = arr;
}
/* 列表容量 */
size(): number {
return this.#tree.length;
}
/* 获取索引为 i 节点的值 */
val(i: number): number | null {
// 若索引越界,则返回 null ,代表空位
if (i < 0 || i >= this.size()) return null;
return this.#tree[i];
}
/* 获取索引为 i 节点的左子节点的索引 */
left(i: number): number {
return 2 * i + 1;
}
/* 获取索引为 i 节点的右子节点的索引 */
right(i: number): number {
return 2 * i + 2;
}
/* 获取索引为 i 节点的父节点的索引 */
parent(i: number): number {
return Math.floor((i - 1) / 2); // 向下整除
}
/* 层序遍历 */
levelOrder(): number[] {
let res = [];
// 直接遍历数组
for (let i = 0; i < this.size(); i++) {
if (this.val(i) !== null) res.push(this.val(i));
}
return res;
}
/* 深度优先遍历 */
#dfs(i: number, order: Order, res: (number | null)[]): void {
// 若为空位,则返回
if (this.val(i) === null) return;
// 前序遍历
if (order === 'pre') res.push(this.val(i));
this.#dfs(this.left(i), order, res);
// 中序遍历
if (order === 'in') res.push(this.val(i));
this.#dfs(this.right(i), order, res);
// 后序遍历
if (order === 'post') res.push(this.val(i));
}
/* 前序遍历 */
preOrder(): (number | null)[] {
const res = [];
this.#dfs(0, 'pre', res);
return res;
}
/* 中序遍历 */
inOrder(): (number | null)[] {
const res = [];
this.#dfs(0, 'in', res);
return res;
}
/* 后序遍历 */
postOrder(): (number | null)[] {
const res = [];
this.#dfs(0, 'post', res);
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
🌙 3.二叉树的遍历O(n)
如何将所有节点都遍历打印出来呢?经典的方法有三种,前序遍历、中序遍历和后序遍历。其中,前、中、后序,表示的是节点与它的左右子树节点遍历打印的先后顺序。
- 前序遍历:根-左-右。对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
- 中序遍历:左-右-根。对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。
- 后序遍历:左-右-根。对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。
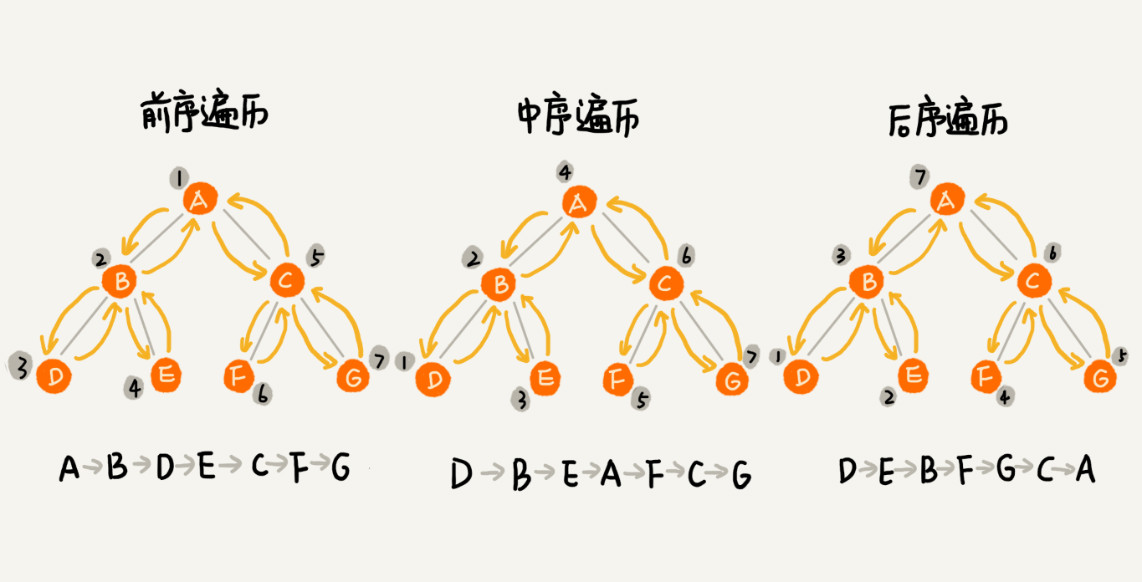
从前、中、后序遍历的顺序图中,可以看出来,每个节点最多会被访问两次,所以遍历操作的时间复杂度,跟节点的个数 n 成正比,也就是说二叉树遍历的时间复杂度是O(n)。
实际上,二叉树的前、中、后序遍历就是一个递归的过程。比如,前序遍历,其实就是先打印根节点,然后再递归地打印左子树,最后递归地打印右子树。
写递归代码的关键,就是看能不能写出递推公式,而写递推公式的关键就是,如果要解决问题 A,就假设子问题 B、C 已经解决,然后再来看如何利用 B、C 来解决 A。所以,我们可以把前、中、后序遍历的递推公式都写出来。
前序遍历的递推公式:
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)
中序遍历的递推公式:
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)
后序遍历的递推公式:
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r
2
3
4
5
6
7
8
🌙 4.二叉树的前序遍历(preOrder) (opens new window)
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var preorderTraversal = function(root) {
let ans = [];
preOrder(root, ans);
return ans;
};
var preOrder = function(root, ans) {
if(!root) return;
// 根 - 左 - 右
ans.push(root.val);
preOrder(root.left, ans);
preOrder(root.right, ans);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
🌙 5.二叉树的中遍历(inOrder) (opens new window)
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var inorderTraversal = function(root) {
let ans = [];
inOrder(root, ans);
return ans;
};
var inOrder = function(root, ans) {
if(!root) return;
// 左 - 根 - 右
inOrder(root.left, ans);
ans.push(root.val);
inOrder(root.right, ans);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
🌙 6.二叉树的后序遍历(postOrder) (opens new window)
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var postorderTraversal = function(root) {
let ans = [];
postOrder(root, ans);
return ans;
};
var postOrder = function(root, ans) {
if(!root) return;
// 左 - 右 - 根
postOrder(root.left);
postOrder(root.right);
ans.push(root.val);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
🌙 7.二叉树的层序遍历(levelOrder) (opens new window)
除了前、中、后序遍历,还可以对二叉树进行层序遍历。层序遍历就是逐层遍历树结构。
广度优先搜索 (opens new window)是一种广泛运用在树或图这类数据结构中,遍历或搜索的算法。从一个根节点开始,首先访问节点本身。 然后遍历它的相邻节点,其次遍历它的二级邻节点、三级邻节点,以此类推。
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number[][]}
*/
var levelOrder = function(root) {
let ans = [];
bfs(root, ans);
return ans;
};
var bfs = function(root, ans) {
if(!root) return;
let queue = [root];
while(queue.length > 0) {
// 记录当前层的数据
let data = [];
// 这里一定要使用固定大小size,不要使用que.size(),因为que.size是不断变化的
let size = queue.length;
for(let i=0; i < size; i++) {
let cur = queue.shift();
data.push(cur.val);
// 左子节点入
if(cur.left) queue.push(cur.left);
// 右子节点入
if(cur.right) queue.push(cur.right);
}
// 保存当前层数据
ans.push(data);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
🌙 8.二叉搜索树(Binary Search Tree) (opens new window)
概念:在二叉树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值 --- 中序遍历的值是一个升序的数据序列
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为 O(logn)
🌙 八、堆Heap (opens new window)
🌙 1.堆的定义
堆 是一种特别的二叉树,满足以下条件的二叉树,可以称之为 堆:
- 完全二叉树;
- 每一个节点的值都必须 大于等于或者小于等于 其孩子节点的值。
堆 具有以下的特点:
- 可以在
O(logN)的时间复杂度内向 堆 中插入元素; - 可以在
O(logN)的时间复杂度内向 堆 中删除元素; - 可以在
O(1)的时间复杂度内获取 堆 中的最大值或最小值。
🌙 2.堆的分类
堆 有两种类型:最大堆 和 最小堆。
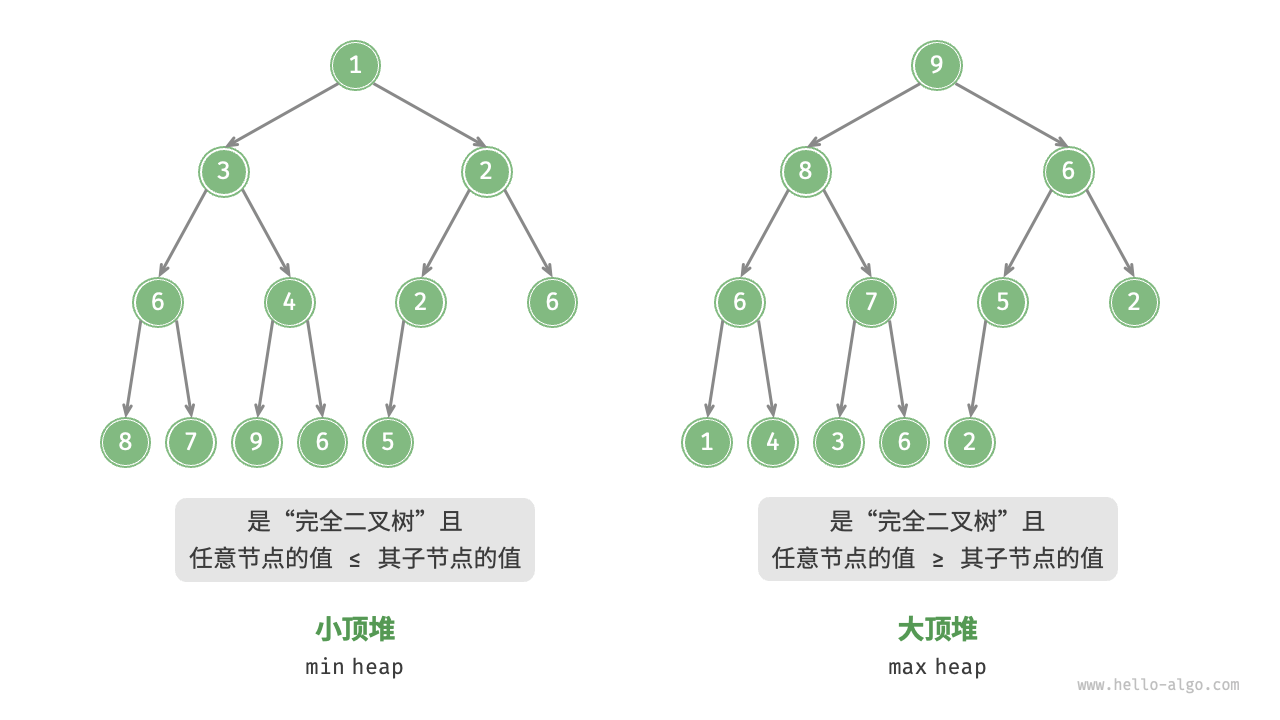
最大堆:堆中每一个节点的值 都大于等于 其孩子节点的值。所以最大堆的特性是 堆顶元素(根节点)是堆中的最大值。
最小堆:堆中每一个节点的值 都小于等于 其孩子节点的值。所以最小堆的特性是 堆顶元素(根节点)是堆中的最小值。
🌙 3.堆的实现
堆通常用于实现优先队列,大顶堆相当于元素按从大到小的顺序出队的优先队列。
push() 元素入堆 𝑂(log 𝑛)
pop() 堆顶元素出堆 𝑂(log 𝑛)
peek() 访问堆顶元素(对于大 / 小顶堆分别为最大 / 小值) 𝑂(1)
size() 获取堆的元素数量 𝑂(1)
isEmpty() 判断堆是否为空 𝑂(1)
2
3
4
5
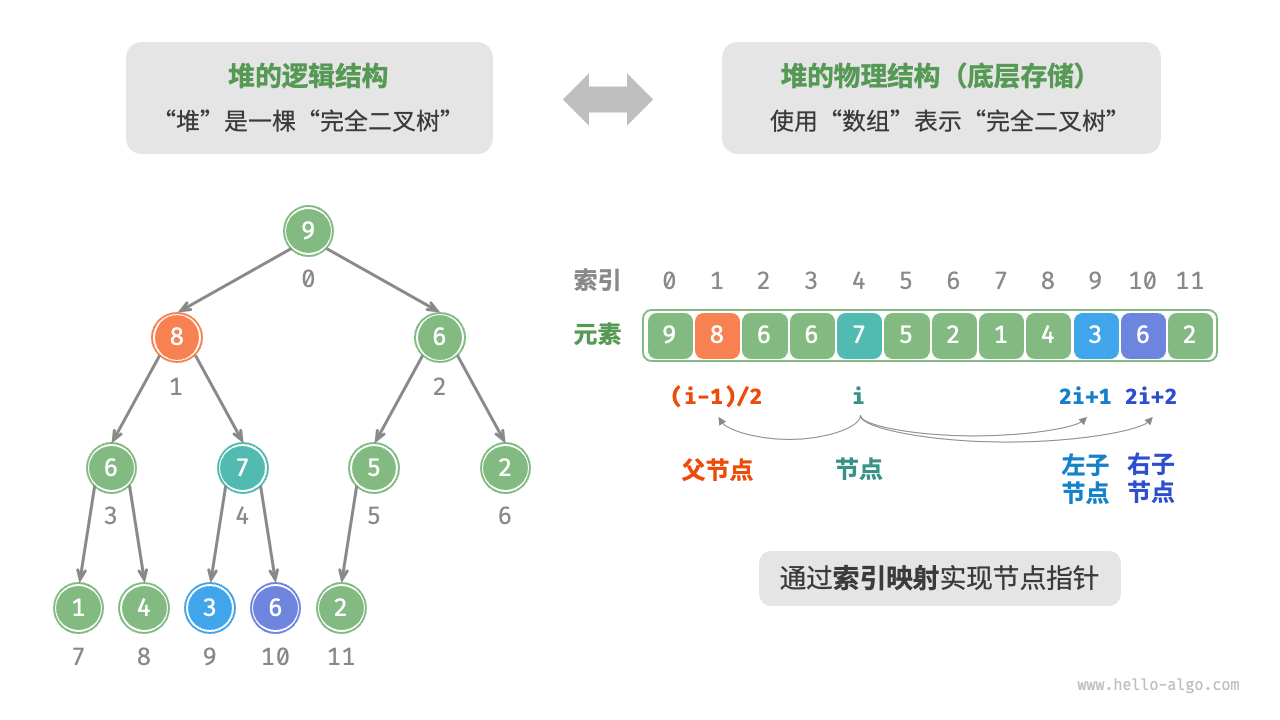
完全二叉树非常适合用数组来表示。由于堆正是一种完全二叉树,因此我们将采用数组来存储堆 。
给定索引𝑖,其左子节点的索引为 2𝑖 + 1 ,右子节点的索引为 2𝑖 + 2 ,父节点的索引为(𝑖 − 1)/2(向下整除)。当索引越界时,表示空节点或节点不存在。
下面实现大顶堆:
/* 最大堆类 */
class MaxHeap {
private maxHeap: number[];
/* 构造方法,建立空堆或根据输入列表建堆 */
constructor(nums?: number[]) {
// 将列表元素原封不动添加进堆
this.maxHeap = nums === undefined ? [] : [...nums];
// 堆化除叶节点以外的其他所有节点
// Math.floor(n / 2) - 1
// Math.floor((n - 1 - 1) / 2)
for (let i = this.parent(this.size() - 1); i >= 0; i--) {
this.siftDown(i);
}
}
/* 获取左子节点的索引 */
private left(i: number): number {
return 2 * i + 1;
}
/* 获取右子节点的索引 */
private right(i: number): number {
return 2 * i + 2;
}
/* 获取父节点的索引 */
private parent(i: number): number {
return Math.floor((i - 1) / 2); // 向下整除
}
/* 交换元素 */
private swap(i: number, j: number): void {
const tmp = this.maxHeap[i];
this.maxHeap[i] = this.maxHeap[j];
this.maxHeap[j] = tmp;
}
/* 获取堆大小 */
public size(): number {
return this.maxHeap.length;
}
/* 判断堆是否为空 */
public isEmpty(): boolean {
return this.size() === 0;
}
/* 访问堆顶元素 */
public peek(): number {
return this.maxHeap[0];
}
/* 元素入堆 */
public push(val: number): void {
// 添加节点
this.maxHeap.push(val);
// 从底至顶堆化
this.siftUp(this.size() - 1);
}
/* 从节点 i 开始,从底至顶堆化 */
private siftUp(i: number): void {
while (true) {
// 获取节点 i 的父节点
const p = this.parent(i);
// 当“越过根节点”或“节点无须修复”时,结束堆化
if (p < 0 || this.maxHeap[i] <= this.maxHeap[p]) break;
// 交换两节点
this.swap(i, p);
// 循环向上堆化
i = p;
}
}
/* 元素出堆 */
public pop(): number {
// 判空处理
if (this.isEmpty()) throw new RangeError('Heap is empty.');
// 交换根节点与最右叶节点(交换首元素与尾元素)
this.swap(0, this.size() - 1);
// 删除节点
const val = this.maxHeap.pop();
// 从顶至底堆化
this.siftDown(0);
// 返回堆顶元素
return val;
}
/* 从节点 i 开始,从顶至底堆化 */
private siftDown(i: number): void {
while (true) {
// 判断节点 i, l, r 中值最大的节点,记为 ma
const l = this.left(i),
r = this.right(i);
let ma = i;
if (l < this.size() && this.maxHeap[l] > this.maxHeap[ma]) ma = l;
if (r < this.size() && this.maxHeap[r] > this.maxHeap[ma]) ma = r;
// 若节点 i 最大或索引 l, r 越界,则无须继续堆化,跳出
if (ma === i) break;
// 交换两节点
this.swap(i, ma);
// 循环向下堆化
i = ma;
}
}
/* 打印堆(二叉树) */
public print(): void {
printHeap(this.maxHeap);
}
/* 取出堆中元素 */
public getMaxHeap(): number[] {
return this.maxHeap;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
🌙 4.大顶堆的使用:
中位数是有序整数列表中的中间值。如果列表的大小是偶数,则没有中间值,中位数是两个中间值的平均值。
例如 arr = [2,3,4] 的中位数是 3 。
例如 arr = [2,3] 的中位数是 (2 + 3) / 2 = 2.5 。
实现 MedianFinder 类:
MedianFinder() 初始化 MedianFinder 对象。
void addNum(int num) 将数据流中的整数 num 添加到数据结构中。
double findMedian() 返回到目前为止所有元素的中位数。与实际答案相差 10-5 以内的答案将被接受。
示例 1:
输入
["MedianFinder", "addNum", "addNum", "findMedian", "addNum", "findMedian"]
[[], [1], [2], [], [3], []]
输出
[null, null, null, 1.5, null, 2.0]
解释
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1); // arr = [1]
medianFinder.addNum(2); // arr = [1, 2]
medianFinder.findMedian(); // 返回 1.5 ((1 + 2) / 2)
medianFinder.addNum(3); // arr[1, 2, 3]
medianFinder.findMedian(); // return 2.0
提示:
-105 <= num <= 105
在调用 findMedian 之前,数据结构中至少有一个元素
最多 5 * 104 次调用 addNum 和 findMedian
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
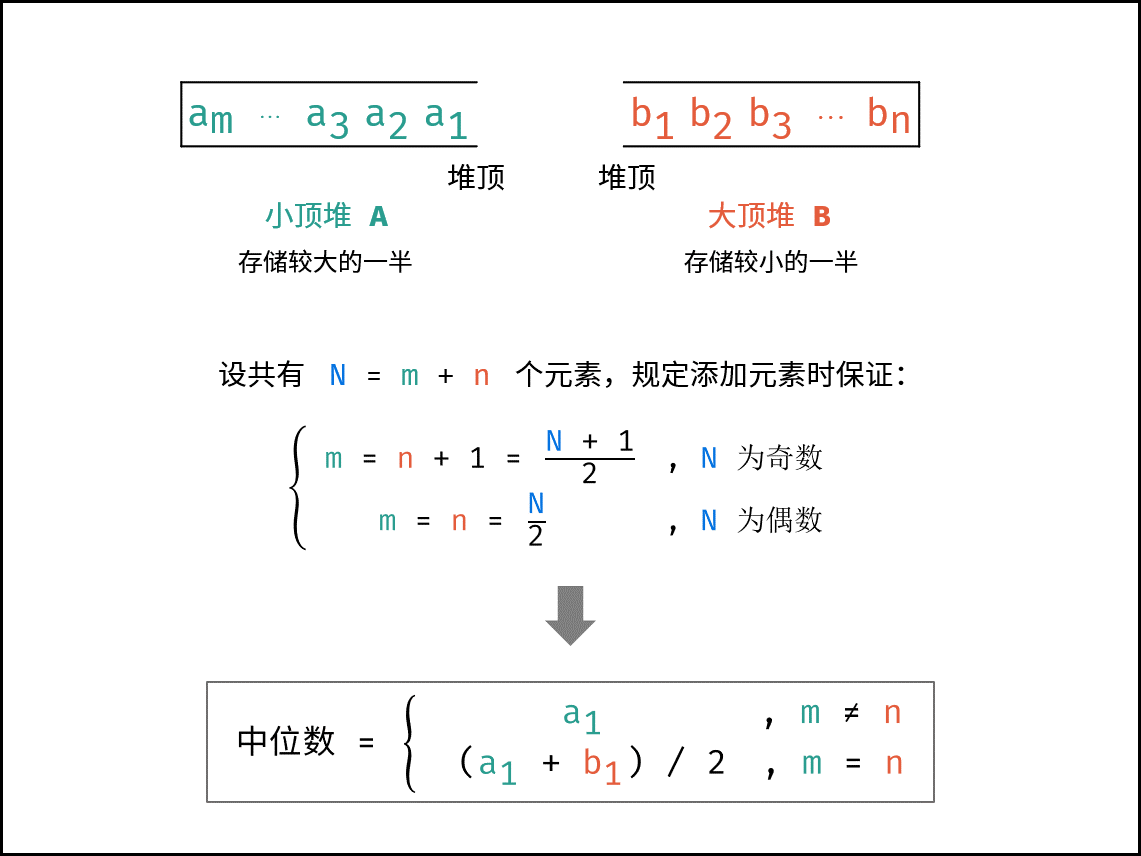
算法实现:
class MedianFinder {
private A: MaxHeap;
private B: MaxHeap;
addNum(num: number): void {
if(this.A.size() === this.B.size()) {
this.B.push(-num)
this.A.push(-this.B.pop())
} else {
this.A.push(num)
this.B.push(-this.A.pop())
}
}
findMedian(): number {
return this.A.size() === this.B.size() ? (this.A.peek() - this.B.peek()) / 2 : this.A.peek()
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18