🌙 二分查找
二分查找算法模板:
查找一维数组arr 中的 target:
// 普通二分查找
function binarySearch(arr, target) {
let left = 0, right = arr.length - 1;
while (left <= right) {
let mid = Math.floor((left + right) / 2);
if (arr[mid] === target) {
return mid
} else if (arr[mid] < target) {
left = mid + 1
} else if (arr[mid] > target) {
right = mid - 1
}
}
return -1
}
// 搜索左侧边界的二分查找1:左闭右开
function leftBoundBinarySearch1(arr, target) {
let left = 0, right = arr.length;
while (left < right) {
let mid = Math.floor((left + right) / 2);
if (arr[mid] === target) {
right = mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else if (arr[mid] > target) {
right = mid;
}
}
return arr[left] === target ? left : -1
}
// 搜索左侧边界的二分查找2:左闭右闭
function leftBoundBinarySearch2(arr, target) {
let left = 0, right = arr.length - 1;
while (left <= right) {
let mid = Math.floor((left + right) / 2);
if (arr[mid] === target) {
right = mid - 1;
} else if (arr[mid] < target) {
left = mid + 1;
} else if (arr[mid] > target) {
right = mid - 1;
}
}
if (left >= arr.length || arr[left] !== target) {
return -1;
}
return left
}
// 搜索右侧边界的二分查找1:左闭右开
function rightBoundBinarySearch1(arr, target) {
let left = 0, right = arr.length;
while (left < right) {
let mid = Math.floor((left + right) / 2);
if (arr[mid] === target) {
left = mid + 1;
} else if (arr[mid] < target) {
left = mid + 1;
} else if (arr[mid] > target) {
right = mid;
}
}
if (left == 0) return -1;
return arr[left - 1] === target ? (left - 1) : -1;
}
// 搜索右侧边界的二分查找2:左闭右闭
function rightBoundBinarySearch2(arr, target) {
let left = 0, right = arr.length - 1;
while (left <= right) {
let mid = Math.floor((left + right) / 2);
if (arr[mid] === target) {
left = mid + 1;
} else if (arr[mid] < target) {
left = mid + 1;
} else if (arr[mid] > target) {
right = mid - 1;
}
}
if (right < 0 || arr[right] !== target) return -1;
return right;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
🌙 案例
🌙 1.搜索二维矩阵 (opens new window)
给你一个满足下述两条属性的 m x n 整数矩阵:
每行中的整数从左到右按非严格递增顺序排列。
每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。
示例 1:
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出:true
示例 2:
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出:false
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-104 <= matrix[i][j], target <= 104
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
- 暴力法
function searchMatrix(matrix, target) {
for (let i = 0; i < matrix.length; i++) {
if (matrix[i].includes(target)) return true
}
return false
}
1
2
3
4
5
6
7
8
2
3
4
5
6
7
8
- 二分查找解法1
第一次:二分查找找到target所在的行
第二次:二分查找找到target所在的列
/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
function searchMatrix(matrix, target) {
let m = matrix.length, n = matrix[0].length
// 找到target所在的行
let left = 0, right = m - 1
while (left <= right) {
let mid = Math.floor((left + right) / 2)
if (matrix[mid][0] === target) {
return true
}
if (matrix[mid][0] < target) {
left = mid + 1
}
if (matrix[mid][0] > target) {
right = mid - 1
}
}
// 判断 是否找到target所在的行
if(right < 0 || matrix[right][0] > target) {
return false
}
if(matrix[right][0] === target) {
return true
}
let row = right
// 找到target所在的列
left = 0, right = n - 1
while (left <= right) {
let mid = Math.floor((left + right) / 2)
if (matrix[row][mid] === target) {
return true
}
if (matrix[row][mid] < target) {
left = mid + 1
}
if (matrix[row][mid] > target) {
right = mid - 1
}
}
let col = right
return matrix[row][col] === target
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
- 二分查找解法2
将二维数组展开为一维数组,直接进行二分查找
/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
function searchMatrix(matrix, target) {
let m = matrix.length, n = matrix[0].length
let left = 0, right = m * n - 1
while (left <= right) {
let mid = Math.floor((left + right) / 2)
let cur = matrix[Math.floor(mid / n)][mid % n]
if (cur === target) {
return true
}
if (cur < target) {
left = mid + 1
}
if (cur > target) {
right = mid - 1
}
}
return false
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
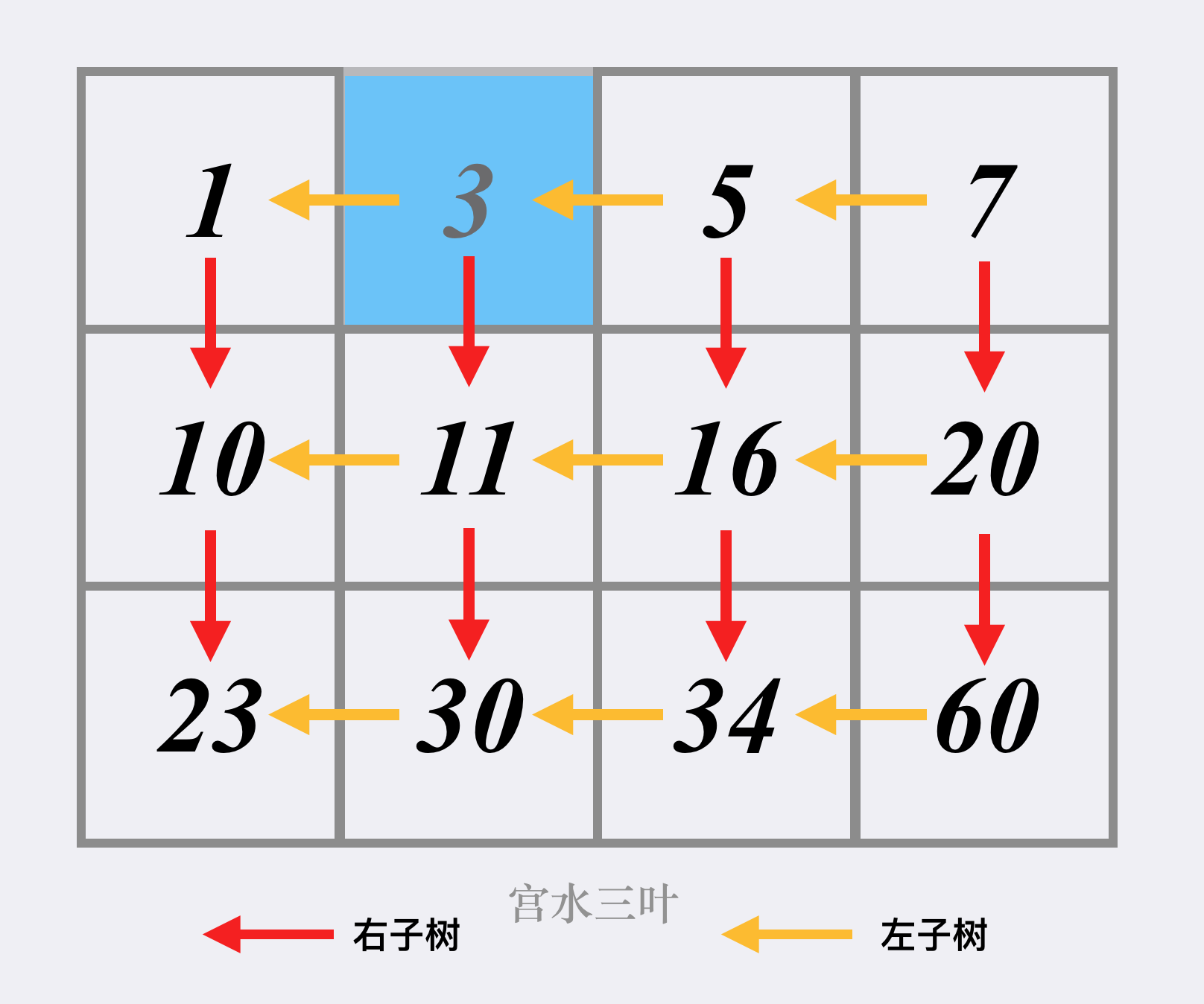
- 二叉搜索树思路
将二维数组看做是以右上角为根节点的二叉树。
/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
function searchMatrix(matrix, target) {
let m = matrix.length, n = matrix[0].length
function isValid(x, y) {
return x >= 0 && x < m && y >= 0 && y < n
}
let row = 0, col = n - 1
while(isValid(row, col) && matrix[row][col] !== target) {
if(matrix[row][col] < target) {
row++
} else {
col--
}
}
return isValid(row, col) && matrix[row][col] === target
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
🌙 2.寻找两个正序数组的中位数 (opens new window)
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
提示:
nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
- 暴力法
先将两个数组合并,然后进行排序,最后取中位数。
function findMedianSortedArrays(nums1: number[], nums2: number[]): number {
// 合并数组, 找到 中间值 空间复杂度: O(m+n) 时间复杂度: O(m+n)
let m = nums1.length, n = nums2.length
let mn = m + n
let arr = []
let i=0, j=0
while(i < m && j < n) {
if(nums1[i] <= nums2[j]) {
arr.push(nums1[i++])
} else {
arr.push(nums2[j++])
}
}
while(i < m) {
arr.push(nums1[i++])
}
while(j < n) {
arr.push(nums2[j++])
}
return (arr[~~((mn - 1)/2)] + arr[~~(mn/2)]) / 2
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
- 优化暴力法
不用排序,只需要找到中位数。
function findMedianSortedArrays(nums1: number[], nums2: number[]): number {
// 直接去找中间值, 时间复杂度 O(m+n) 空间复杂度 O(1)
let m = nums1.length, n = nums2.length
let mn = m+n
// 分别记录左右中间值
let left = 0, right = 0
// 遍历下标
let i = 0, j = 0
// 中间下标
let mid = ~~(mn / 2)
for(let k=0; k<=mid; k++) {
// left 记录 right 之前的值, 保证 left 总是 right上一个值,便于计算中位数(偶数个数的时候)
left = right
// 下面更新right的值
if(i < m && (j >=n || nums1[i] < nums2[j])) {
right = nums1[i++]
} else {
right = nums2[j++]
}
}
return mn % 2 === 0 ? (left + right) / 2 : right
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
- 二分法
function findMedianSortedArrays(nums1: number[], nums2: number[]): number {
let m = nums1.length, n = nums2.length
let mn = m+n
if(mn % 2 === 0) {
return (findKthNum(nums1, nums2, mn / 2) + findKthNum(nums1, nums2, mn / 2 + 1)) / 2
} else {
return findKthNum(nums1, nums2, (mn + 1) / 2)
}
};
function findKthNum(n1: number[], n2: number[], k: number): number {
let s1 = 0, e1 = n1.length - 1
let s2 = 0, e2 = n2.length - 1
// [s1, ..., mid1, ..., e1]
// [s2, ..., mid2, ..., e1]
while(s1 <=e1 && s2 <= e2) {
let mid1 = ~~((s1 + e1) / 2)
let mid2 = ~~((s2 + e2) / 2)
let c1 = mid1 - s1 + 1
let c2 = mid2 - s2 + 1
// 将 n1 和 n2 分成两半,每次判断 k 落在哪半部分,缩小范围
if(n1[mid1] <= n2[mid2]) {
if(c1 + c2 > k) {
// nums2 取前半部分
e2 = mid2 - 1
} else {
// nums1 取后半部分,并缩小k值
k -= (mid1 - s1 + 1)
s1 = mid1 + 1
}
} else {
if(c1 + c2 > k) {
// nums1 取前半部分
e1 = mid1 - 1
} else {
// nums2 取后半部分,并缩小k值
k -= (mid2 - s2 + 1)
s2 = mid2 + 1
}
}
}
if(s1 > e1) {
return n2[s2 + k - 1]
} else {
return n1[s1 + k - 1]
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
🌙 3.两数相除 (opens new window)
给你两个整数,被除数 dividend 和除数 divisor。将两数相除,要求 不使用 乘法、除法和取余运算。
整数除法应该向零截断,也就是截去(truncate)其小数部分。例如,8.345 将被截断为 8 ,-2.7335 将被截断至 -2 。
返回被除数 dividend 除以除数 divisor 得到的 商 。
注意:假设我们的环境只能存储 32 位 有符号整数,其数值范围是 [−231, 231 − 1] 。本题中,如果商 严格大于 231 − 1 ,则返回 231 − 1 ;如果商 严格小于 -231 ,则返回 -231 。
示例 1:
输入: dividend = 10, divisor = 3
输出: 3
解释: 10/3 = 3.33333.. ,向零截断后得到 3 。
示例 2:
输入: dividend = 7, divisor = -3
输出: -2
解释: 7/-3 = -2.33333.. ,向零截断后得到 -2 。
提示:
-231 <= dividend, divisor <= 231 - 1
divisor != 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
- 迭代法(会超时)
function divide(dividend: number, divisor: number): number {
// 迭代法
if(dividend === 0) {
return 0
}
// 除数不能为0
if(divisor === 0) {
return NaN
}
if(divisor === 1) {
return dividend
}
// 32位有符号整数,溢出处理
if(dividend === -2147483648 && divisor === -1) {
return 2147483647
}
let res = 0
// 判断正数还是负数
let flag = 1
if (dividend < 0) {
flag *= -1
dividend = -dividend
}
if (divisor < 0) {
flag *= -1
divisor = -divisor
}
while (dividend >= divisor) {
// 每次减去除数
dividend -= divisor
res++
}
return flag === 1 ? res : -res
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
- 倍增乘法: 每次用被除数减去
除数的最大的2^x
function divide(dividend: number, divisor: number): number {
// 处理溢出
if (dividend === -2147483648 && divisor === -1) {
return 2147483647
}
// 记录符号
let flag = -1
if(dividend > 0 && divisor > 0 || dividend < 0 && divisor < 0) {
flag = 1
}
// 全部转为正数
dividend = Math.abs(dividend)
divisor = Math.abs(divisor)
let ans = 0
// 每次减去除数的 2^x 倍数,以此类推
while(dividend >= divisor) {
let temp = divisor
let i = 1
while(temp <= dividend - temp) {
temp += temp
i += i
}
// 被除数减去除数的 2^x 倍数做为新的被除数
dividend -= temp
ans += i
}
return flag < 0 ? -ans : ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
- 二分法:
function divide(dividend: number, divisor: number): number {
// 处理溢出
if (dividend === -2147483648 && divisor === -1) {
return 2147483647
}
if (dividend === 0) return 0;
if (divisor === 1) return dividend;
// 记录符号
let flag = dividend > 0 === divisor > 0
// 全部转为正数
dividend = Math.abs(dividend)
divisor = Math.abs(divisor)
// 答案一定在区间[0, dividend]之间, 由于是向下取整,我们找左侧边界
let left = 0, right = dividend
while (left < right) {
// 二分查找
let mid = left + right + 1 >> 1
if (quickMulti(divisor, mid) <= dividend) {
left = mid
} else {
right = mid - 1
}
}
// 快速乘法 x*y = x + x + ... + x (y次)
function quickMulti(x: number, y: number) {
let ans = 0
while (y > 0) {
// y & 1 === 1 表示最低位为1
if ((y & 1) === 1) {
ans += x
}
// x * 2
x <<= 1
// y / 2
y >>= 1
}
return ans
}
return flag ? left : -left
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
- 递归:
function divide(dividend: number, divisor: number): number {
// 32 位的有符号整数
const MAX_VALUE = 2 ** 31 - 1, MIN_VALUE = -(2 ** 31);
// 考虑被除数为最小值的情况
if (dividend === MIN_VALUE) {
if (divisor === 1) {
return MIN_VALUE;
}
if (divisor === -1) {
return MAX_VALUE;
}
}
// 考虑除数为最小值的情况
if (divisor === MIN_VALUE) {
return dividend === MIN_VALUE ? 1 : 0;
}
// 考虑被除数为 0 的情况
if (dividend === 0) {
return 0;
}
// 全部转为负数,避免溢出
if (dividend > 0) return -divide(-dividend, divisor);
if (divisor > 0) return -divide(dividend, -divisor);
if (dividend > divisor) return 0;
let res = 1, tmp = divisor;
while ((dividend - divisor) <= divisor) {
res += res;
divisor += divisor;
}
return res + divide(dividend - divisor, tmp);
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
🌙 4.搜索旋转排序数组 (opens new window)
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [1], target = 0
输出:-1
提示:
1 <= nums.length <= 5000
-104 <= nums[i] <= 104
nums 中的每个值都 独一无二
题目数据保证 nums 在预先未知的某个下标上进行了旋转
-104 <= target <= 104
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
- 暴力法
function search(nums: number[], target: number): number {
for(let i=0; i<nums.length; i++) {
if(nums[i] === target) return i
}
return -1
}
1
2
3
4
5
6
7
2
3
4
5
6
7
二分法
不管怎么进行旋转,数组都会被分为有序的两部分,每次进行二分前比较一下中间索引与左右边界的值,如果
nums[m]>=nums[left],则索引左边有序,否则右边有序。
function search(nums: number[], target: number): number {
let len = nums.length;
if (len === 0) {
return -1;
}
if (len === 1) {
return nums[0] === target ? 0 : -1;
}
let left = 0, right = len - 1;
// 二分法
while (left <= right) {
let mid = (left + right) >> 1;
// 找到了,直接返回
if (nums[mid] === target) {
return mid;
}
// 原数组 1,2,3,4,5,6
// 旋转后 5, 6, 1,2,3,4
// 旋转后 4, 5, 6, 1,2,3
// 旋转后 6, 1,2,3,4,5
// 由于是升序排序,旋转之后只需要判断 nums[mid] > nums[left], 那么mid左边就是有序的,反之,右边有序
if(nums[mid] >= nums[left]) {
if(nums[left] <= target && target < nums[mid]) {
right = mid - 1;
} else {
left = mid + 1;
}
} else {
if(nums[mid] < target && target <= nums[right]) {
left = mid + 1;
} else {
right = mid - 1;
}
}
}
return -1;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
🌙 5.在排序数组中查找元素的第一个和最后一个位置 (opens new window)
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
提示:
0 <= nums.length <= 105
-109 <= nums[i] <= 109
nums 是一个非递减数组
-109 <= target <= 109
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
非递减排列:指一个数列中的元素从左到右依次不减,或者说不降序排列。也就是说,如果数列中某个元素的值比它前面的元素小,那么它的值至少和前面的元素相等,即数列中不存在逆序对。如果数列中有相邻的元素相等,也认为是非递减排列。简单理解为 升序排列,但存在相等。
- 直接使用 JS api:
function searchRange(nums: number[], target: number): number[] {
// 使用 js api
let left = nums.indexOf(target)
let right = nums.lastIndexOf(target)
return [left, right]
};
1
2
3
4
5
6
7
2
3
4
5
6
7
- 经典二分:
function searchRange(nums: number[], target: number): number[] {
if(nums.length < 1) return [-1, -1]
// leftBoundBinarySearch 和 rightBoundBinarySearch 见前面的实现
let left = leftBoundBinarySearch(nums, target)
let right = rightBoundBinarySearch(nums, target)
return [left, right]
};
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9